���}Ŀ��ij�������Ƴ�һ�l�ɱ��r(ji��)λ500Ԫ/�˵�ʡ��(n��i)���ξ�·�������ο��˔�(sh��)y����/�£��c���Έ�(b��o)�r(ji��)x��Ԫ/�ˣ�֮�g���P(gu��n)ϵ��y=��x+1300�������֪���������ܲ��TҎ(gu��)��ԓ���ξ�·��(b��o)�r(ji��)��800Ԫ/�ˡ�1200Ԫ/��֮�g��
��1��Ҫ��ԓ���ξ�·ÿ���ο��˔�(sh��)������200���ԃ�(n��i)����ԓ���ξ�·��(b��o)�r(ji��)��ȡֵ���������
��2����(j��ng)�I(y��ng)�@�l���ξ�·ÿ������Ҫ����ͳɱ��������
��3���n�@�l���ξ�·�����Έ�(b��o)�r(ji��)����ٕr(sh��)�������ɫ@���������(r��n)���������(r��n)�Ƕ�������
���𰸡���1��ȡֵ������1100Ԫ/�ˡ�1200Ԫ/��֮�g��������2��50000����3��x=900�r(sh��)�������w���=160000
��������ԇ�}��������1������(j��)�}���в���ʽ�����������
��2������(j��)��(b��o)�r(ji��)�pȥ�ɱ��ɵõ�����(sh��)�Ľ���ʽ����������(j��)һ�κ���(sh��)�ĈD����⼴�ɣ�
��3������(j��)����(r��n)�����˴γ��ԃr(ji��)�ɵõ�����(sh��)�Ľ���ʽ�������Ȼ�����(j��)���κ���(sh��)����ֵ��⼴��.
ԇ�}��������1�������}���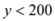 �r(sh��)�����
�r(sh��)�����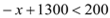 ��
��
����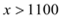
��Ҫ��ԓ���ξ�·ÿ���ο��˔�(sh��)������200���ԃ�(n��i)����ԓ���ξ�·��(b��o)�r(ji��)��ȡֵ������1100Ԫ/��~1200Ԫ/��֮�g��
��2�� ������
������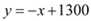 ����
����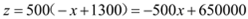
��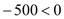 �������ஔ(d��ng)
�������ஔ(d��ng)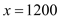 �r(sh��)��z�����������
�r(sh��)��z�����������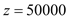 ��
��
��3������(r��n)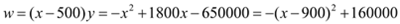
��(d��ng)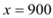 �r(sh��)�����
�r(sh��)�����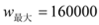 .
.
���}�͡�����}
���Y(ji��)����
23
���}Ŀ����֪��߅��ABCD���������AB=AD����(du��)�Ǿ�ACƽ�֡�DAB�������^(gu��)�c(di��n)C��CE��AB���c(di��n)E���c(di��n)F��AB��һ�c(di��n)�������EF=EB�������B��DF��
��1�����C��CD=CF��
��2���B��DF�������AC���c(di��n)G�������C����DGC����ADC���
��3�����c(di��n)H�龀��DG��һ�c(di��n)��������B��AH����������ADC=2��HAG��AD=3����DC=2��������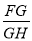 ��ֵ��
��ֵ��